Adaptive Learning Rate in Deep Learning

Adaptive learning rate algorithms monitor the performance of the training and based on monitoring they adjust learning rate. They provide heuristic approach without requiring expensive work in tuning hyperparameters for the Learning rate schedule manually.

The issue with Learning rate schedules is that they all depend on hyperparameters that must be manually chosen for each given learning session and may vary greatly depending on the problem at hand or the model used. This issue is solved by Adaptive learning rate algorithms.

See what is Learning rate schedules here https://marko-kovacevic.com/blog/learning-rate-schedules-in-deep-learning/ .

Instead of manually updating Learning rate value after training by yourself, algorithms can do it for you during training based on heuristic approach.

The most popular Adaptive learning rate algorithms are: Adagrad, RMSprop and Adam. It is interesting that RMSprop is created from Adagrad and Adam is created from RMSprop.

1. Adagrad

Adagrad is Adaptive learning rate algorithm and it adapts learning rate to the parameters.

A downside of Adagrad is that in case of Deep Learning, the learning rate usually proves too aggressive and stops learning too early.

1.1. Matematical Implementation

cache = cache + dx**2
x = x - learning_rate * dx / (np.sqrt(cache) + epsilon)

cache – keeps track of per-parameter sum of squared gradients and then it is used to normalize the parameter update step, element-wise

epsilon – avoids division by zero and usually it is set somewhere in range from 1e-4 to 1e-8

** – square

Square root operation turns out to be very important and without it the algorithm performs much worse.

Weights that receive high gradients will have their effective learning rate reduced, while weights that receive small or infrequent updates will have their effective learning rate increased.

1.2. Programming Implementation

Keras:

tf.keras.optimizers.Adagrad(
    learning_rate=0.001, initial_accumulator_value=0.1, epsilon=1e-07,
    name='Adagrad', **kwargs
)

https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Adagrad

2. RMSprop

RMSprop stands for Root mean square propagation. It was invented by Geoffrey Hinton and fun fact is that it was not first proposed in academic research paper but in a Geoffrey Hinton Coursera class.

The RMSProp update adjusts the Adagrad algorithm in an attempt to reduce its aggressive, monotonically decreasing learning rate.

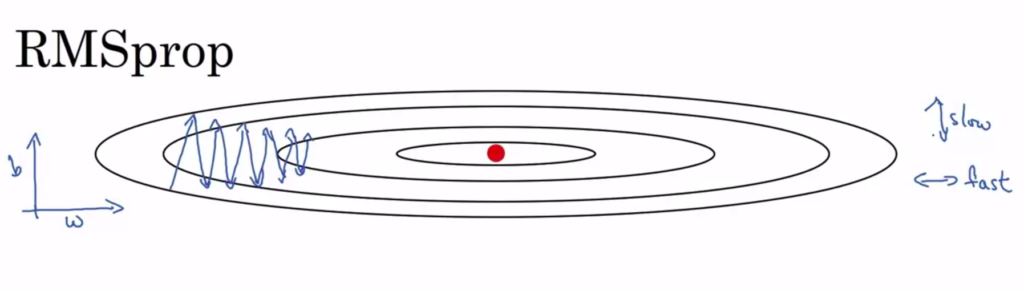
RMSprop slow learning in vertical direction and speed learning in horizontal direction.

It is called Root mean square propagation because it squaring derivatives and then take square root at the end.

2.1. Mathematical Implementation

w_cache = decay_rate * w_cache + (1 - decay_rate) * dw**2
w = w - learning_rate * dw / (np.sqrt(w_cache) + epsilon)

b_cache = decay_rate * b_cache + (1 - decay_rate) * db**2
b = b - learning_rate * db / (np.sqrt(b_cache) + epsilon)

decay_rate – hyperparameter and typical values are [0.9, 0.99, 0.999]

epsilon – avoids division by zero and usually it is set somewhere in range from 1e-4 to 1e-8

** – square

We are making w_cache to be small number to make faster learning in horizontal direction.

We are making b_cache to be large number to make slower learning in vertical direction.

Variables w and b are used only to ilustrate horizontal and vertical dimensions in practice it is a very high dimensional space of parameters, maybe vertical dimensions are sum set of parameters w1,w2, w17 and the horizontal dimensions might be sum set of parameters w3, w4, w5.

2.2. Programming Implementation

Keras:

tf.keras.optimizers.RMSprop(
    learning_rate=0.001, rho=0.9, momentum=0.0, epsilon=1e-07, centered=False,
    name='RMSprop', **kwargs
)

https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/RMSprop

3. Adam

Adam stands for Adaptive Moment Estimation . It is combination of Momentum and RMSprop algorithms.

See what is Momentum here https://marko-kovacevic.com/blog/momentum-in-deep-learning/ .

It is most used optimisation algorithm because it oftes gives best results.

3.1. Mathematical Implementation

m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)

v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)

x = x - learning_rate * mt / (np.sqrt(vt) + epsilon)

beta1 – hyperparameter and recommended value is 0.9

beta2 – hyperparameter and recommended value is 0.999

epsilon – avoids division by zero and recommended value is 1e-8

m – Adam parameter, Momentum update

v – Adam parameter, RMSprop update

mt, vt – Adam parameters with Bias correction

** – square

3.2. Programming Implementation

Keras:

tf.keras.optimizers.Adam(
    learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False,
    name='Adam', **kwargs
)

https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Adam

Thanks for reading this post.

References

1. Cs231n.github.io. 2020. Stanford University – Cs231n Convolutional Neural Networks For Visual Recognition. [online] Available at: <https://cs231n.github.io/neural-networks-3/> [Accessed 13 June 2020].
2. Coursera. 2020. Rmsprop – Optimization Algorithms | Coursera. [online] Available at: <https://www.coursera.org/learn/deep-neural-network/lecture/BhJlm/rmsprop> [Accessed 13 June 2020].
3. Coursera. 2020. Adam Optimization Algorithm – Optimization Algorithms | Coursera. [online] Available at: <https://www.coursera.org/learn/deep-neural-network/lecture/w9VCZ/adam-optimization-algorithm> [Accessed 15 June 2020].
4. En.wikipedia.org. 2020. Learning Rate. [online] Available at: <https://en.wikipedia.org/wiki/Learning_rate> [Accessed 15 June 2020].